Singly Linked List

Introduction

Have you ever wandered through Instagram feeds? Yeah, one image after another it keeps on scrolling, it’s infinite, it’s almost never-ending!

But have you ever wondered how it all works? Imagine, if you were the engineer who was asked to develop this feature, how would you have approached this problem?

How would have you maintained the huge collection of images?

The first thing that would have crossed your mind is maintaining an array of all images, but what if the number of images is ever increasing? Soon you’ll realize that arrays are not suited for this job, they don’t go very well with dynamic size data.

We need something better, we need a data structure that can store a collection of objects just like an array, but whose size can be manipulated in real-time. This is where the Linked List comes in.

What is a Linked List?

A Linked List is a sequence of elements such that each element in the linked list points to the adjacent element in the sequence.

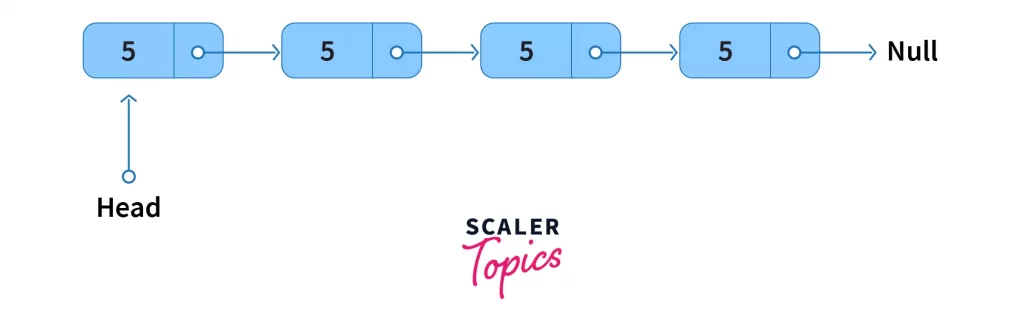
Each element of the Linked List is called a Node. A Linked List is formed by connecting multiple nodes.

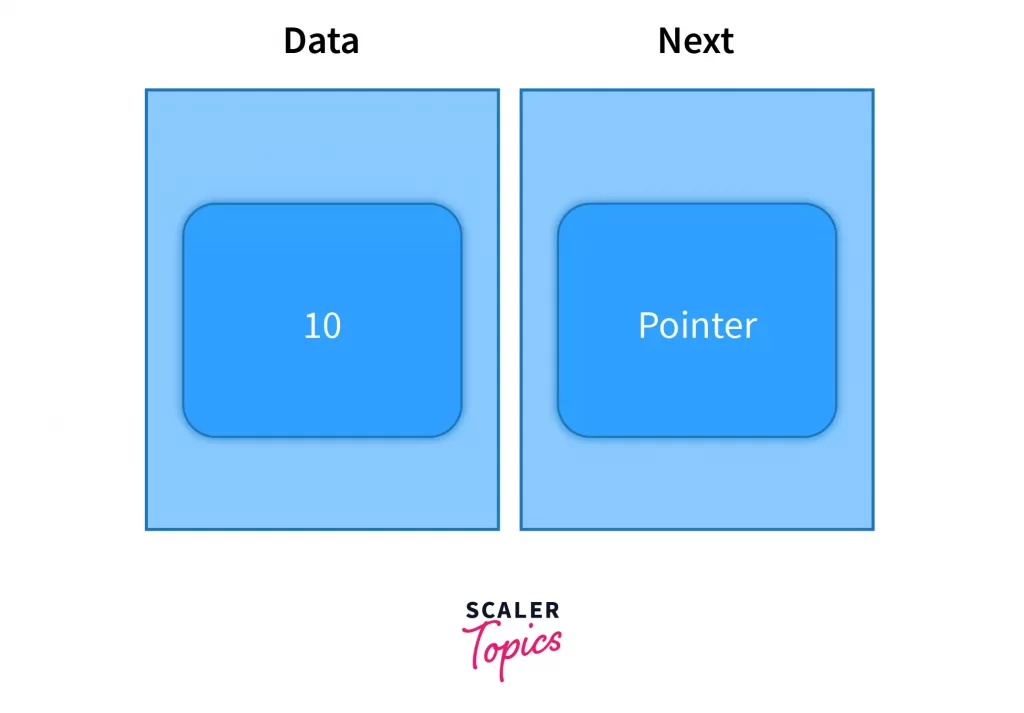
A node consists of two parts,

1. Data: It is the actual raw information that you want to maintain. It can be a video object, a number, a character, etc.
2. Pointer to another node: It stores the link of the adjacent node.

Why use a linked list over an array?

• Dynamic Size Array’s have a fixed size. Once the size of an Array is defined, it can’t be modified. However the size of the linked list can be changed during the runtime.

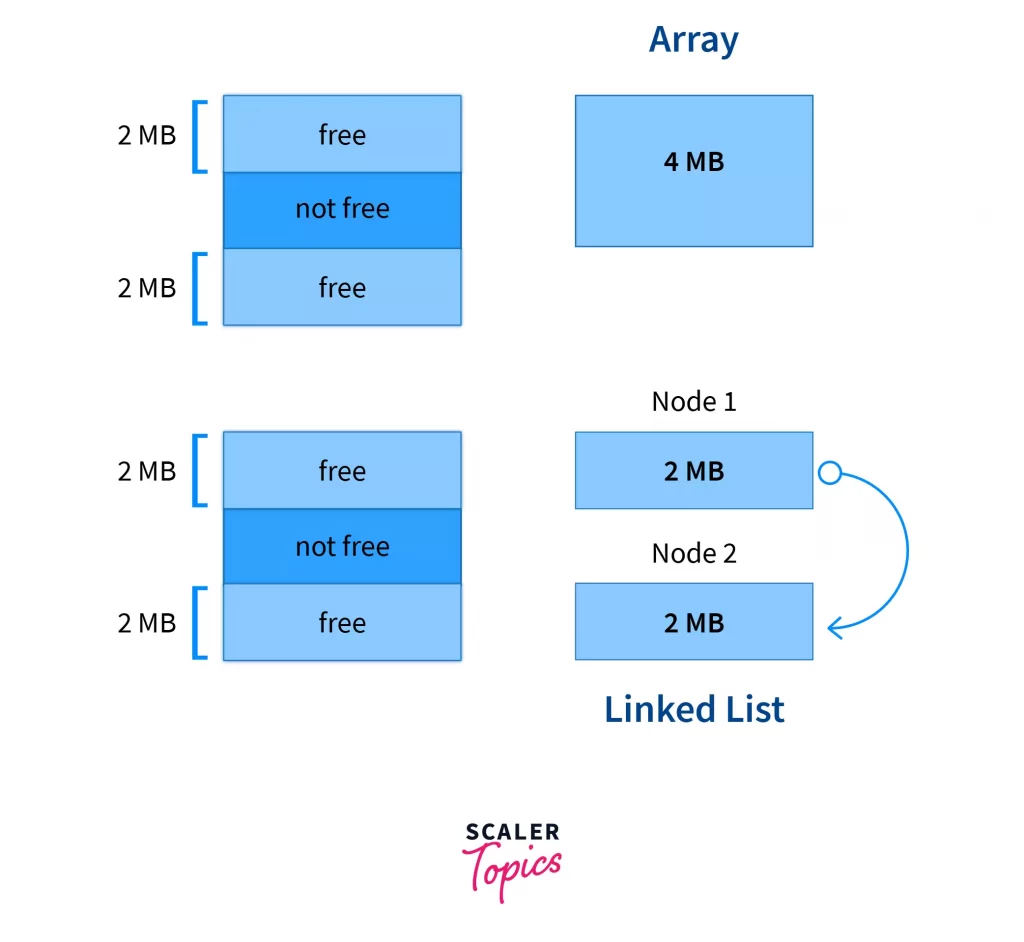
• Memory Consumption Arrays requires memory allocation in a contiguous manner. While for linked list memory can be allocated dynamically. All the nodes of a linked list are stored at non-contiguous memory locations and are linked by pointers.

  For ex: Assume the system has 4MB of free space available. However, the free space is in a noncontiguous manner. Now we can easily store up to 4MB of linked list inside this space but 4MB of array cannot be accommodated. Hence linked list exploit memory to its full potential.

• Fast Insertion/Deletion Time complexity of deletion and insertion in an array is O(N). Whereas in linked list deletion and insertion can be done in O(1).

What is a singly linked list?

A Singly Linked List is a specialized case of a generic linked list. In a singly linked list, each node links to only the next node in the sequence, i.e if we start traversing from the first node of the list, we can only move in one direction(pun intended).

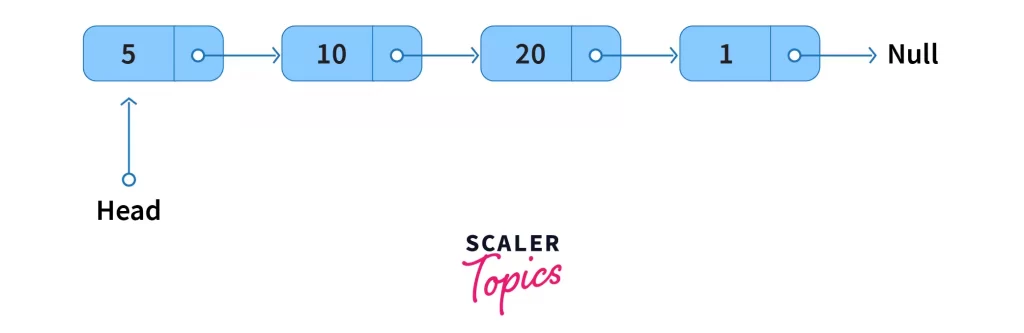
The Node of the singly linked list, apart from the data, stores the address of only the next element, as shown below. The following is the JAVA representation of a node.

For a linked list we maintain a special pointer known s HEAD. Thispointer stores the address of the first node of the list. Also, the last node can no longer have the next element. Hence we indicate the end of the linked list by assigning NULL to its next.

Operations on singly linked list

1. Insertion

Insertion in a singly linked list can be performed in the following ways,

• Insertion at the start Insertion of a new node at the start of a singly linked list is carried out in the following manner.
  • Make the new node point to HEAD.
  • Make the HEAD point to the new node.

Inserting a new node at the start is an O(1) operation.

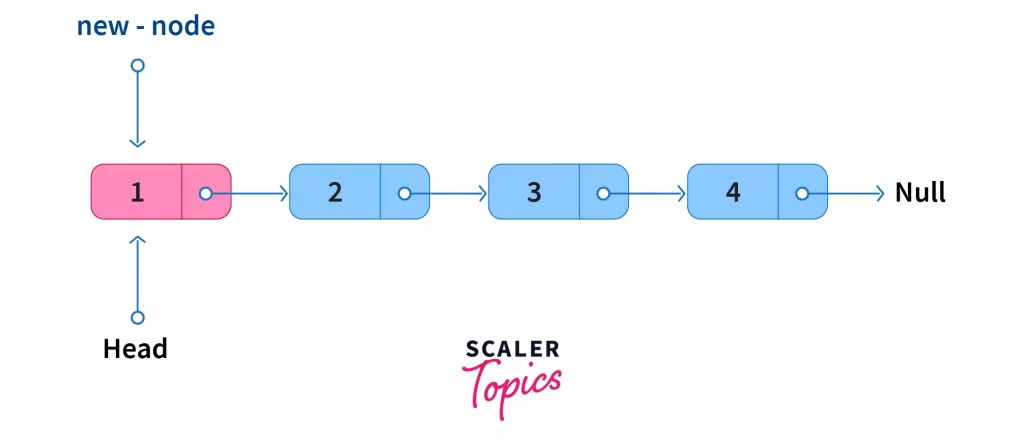
• Insertion after some Node Insertion of a new node after some node in a singly linked list is carried out in the following manner,
  • Reach the desired node after which the new node is to be inserted.
  • Make the new node point to the next element of the current node.
  • Make the current node point to the new node. Inserting a new node after some node is an O(N) operation.

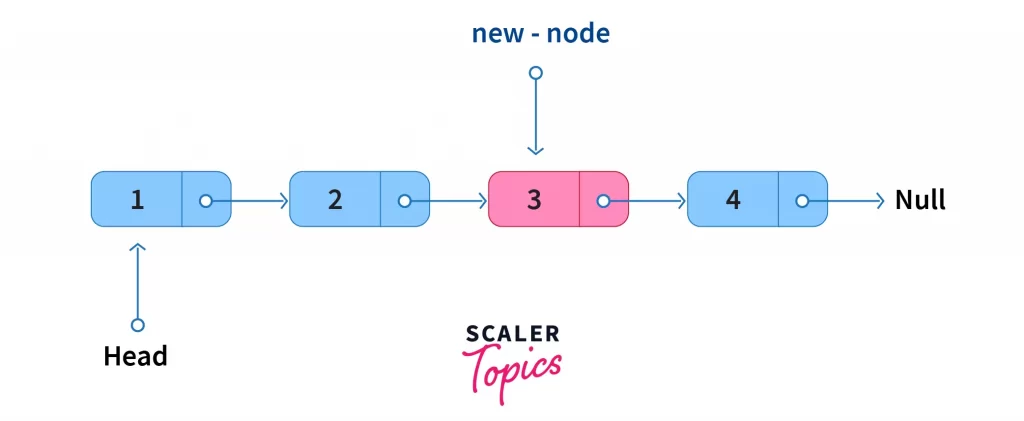
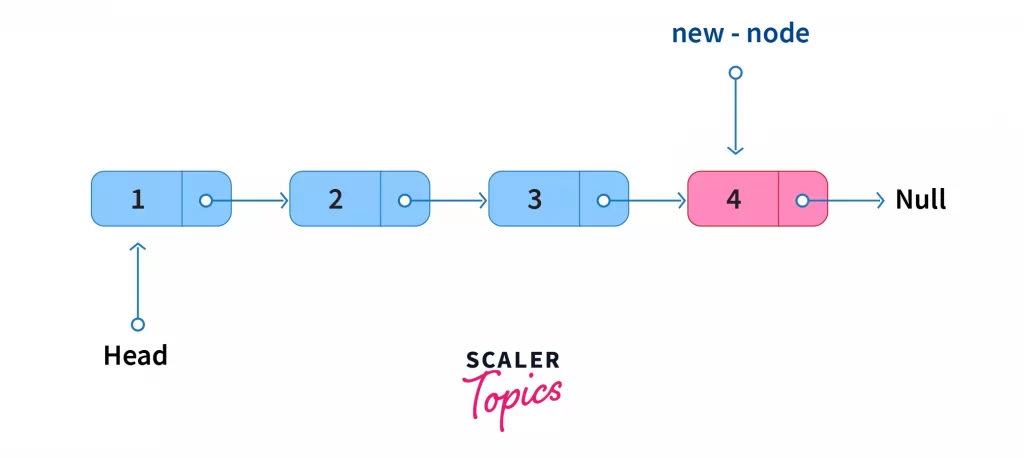
• Insertion at the end Insertion of a new node at the end of a singly linked list isperformed in te followin way,
  • Taverse the list from start and reach the last node.
  • Make the last node point to the new node.
  • Make the new node point to null, marking the end of the list. Inserting a new node at the end is an O(N) operation.

2. Deletion

Deletion in a singly linked list can be performed in the following ways,

• Deletion at the start
  The first node of the singly linked list can be deleted as follows,

  • Make the HEAD point to its next element.

Deleting the first node of a singly linked list is an O(1) operation.

• Deletion at the middle

The deletion after a specific node can be formed in the following way,

• Reach the desired node after which the node is to be deleted.
• Make the current node point to the next of next element.

Deleting a node after a specific node is an O(N) operation.

• Deletion at last

The deletion of the last node is performed in the following manner,

• Reach the second last node of th singly linke list.
• Make the second last node point null.

Deleting the last node is an O(N) operation.

3. Display

To display the entire singly linked list, we need to traverse it from first to last.

In contrast to arrays, linked list nodes cannot be accessed randomly. Hence to reach the n-th element, we are bound to traverse through all (n-1) elements.

Since the entire linked list is traversed, the operation costs us O(N) time complexity. The following JAVA snippet shows how the entire singly linked list can be displayed.

4. Search

To search an element in the singly linked list, we need to traverse the linked list right from the start.

At each node, we perform a lookup to determine if the target has been found, if yes, then we return the target node else we move to the next element.

In the worst case, we could end up visiting all the nodes in the list and hence searching an element in the singly linked list cost us O(N) operational time.

Can we do better?

Assume that the entire singly linked list is already sorted in ascending manner. Can we apply the binary search on Linked List and complete our searching operation in O(log N) time?

It turns out we can’t, even if the linked list is already sorted we cannot perform the binary search over it. One of the important things for the binary search to work on a collection is, any location of the collection must be randomly accessible in constant time. Arrays obey this property as we can access specifically any array element in constant time.

However, with Linked List such random access is prohibited. Any element of a singly linked list can only be accessed in a sequential manner making binary search completely ineffective.

Uses of Linked List

Some of the real-life applications of the linked list are as follows:

• Used to store single or bivariable polynomials.
• Act as a base for certain data structures like Queue, Stack, Graph.
• Strategy for file allocation schemes by Operating System.
• Keep track of free space in the secondary disk. All the free spaces can be linked together.
• Turn-based games can use a circular linked list to decide which player is about to be played. Once the player finishes its turn we move to the next player.
• To keep records of items such as music, videos, images, web pages, etc which link to one another and allows to traverse between them sequentially.